バカテスト・物理

（ライトノベル『バカとテストと召喚獣8』（第8巻） pp.228-229）
最終問題（第６問）

問　以下の問いに答えなさい。
　木の上にいる猿に向けて射手が同じ高さから銃を撃ったところ、発射と同時に猿の足元の枝が折れて猿が落下し始めた。この時、猿と弾丸はどうなるか。必要であれば以下の値を用いて説明しなさい。
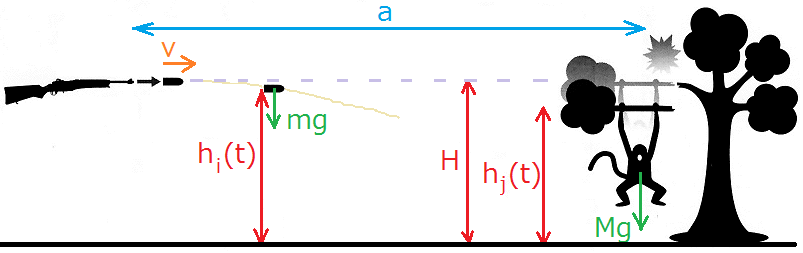
　猿と射手の距離を a とし、最初に猿がいた枝の高さを H 、弾丸が猿のいた木に到達するまでの時間を t 、その時の弾丸の高さを h(i) 、その時の猿の高さを h(j) 、弾丸の速度を v 、重力加速度を g とする。尚、空気抵抗は存在しないものとする。

＜姫路瑞希の答え＞

　h(i) = H - 1/2 gt²
　h(j) = H - 1/2 gt²

よって、

h(i) = h(j)
『このことから、猿と弾丸の高さは常に一致するので、弾丸は猿に当たると言える。』

＜Chemquriy的な答え（模範解答）＞

　弾丸と猿はどちらも地面に垂直な方向に初速度を持っておらず、かつ両者とも重力のみしか作用しないので、両者の高さは常に等しい。

よって、

　h(i) = h(j)

が言えるが、これが成り立つのは、h(i) = h(j) ≧ 0 の場合に限る。

（中略：下で解説する）

以上より、

H ≧ 1/2 g・(a/v)² のとき、弾丸は猿に衝突する。
H ＜ 1/2 g・(a/v)² のとき、猿は弾丸に衝突される前に地面に着いてしまい、その場に猿が留まったとすると、弾丸は猿の頭上を通過する。

＜解説＞

本問は「モンキーハンティング」（略称：「モンハン」　愛称：「サルゲッチュ」）と呼ばれる問題の特殊形です。モンキーハンティングとは、ハンターが地面から木の上の猿を狙う際に、初速度や角度などの条件をどう設定したらいいかな、というのを考える物理実験問題です。モンハンにおいては、猿は弾丸が迫っていようが緊急回避をすることもなく、ただ重力に従って自由落下するだけであると仮定されます。さらに空気抵抗や風などの面倒くさい現象を一切無視することによって、中学高校レベルの簡単な物理計算でサルをに弾丸を衝突させるための条件が求めることができる、というわけです。本問は、ハンターは地面から虎視眈々と猿を狙っているのではなく、猿と同じ高さでハンターは弾丸を射出するので、モンキーハンティングにおけるθ＝０の場合と考えることができます。（詳しくは、後述する「モンキーハンティング」を参照。）

でも、弾丸が猿に衝突する前に、猿が地面に着いてしまったら意味がありませんよね（爆）。

揚げ足取りかと思うかもしれませんが、与えられた問題に対して可能な限りの解を提示するのが理科ってもんです。というか、そうしないと普通はバツですよ！！　理科の世界は厳しいのです。

本問ではわざわざ射手と猿の初期状態での距離が提示されています。「教師のコメント」で、教師は a は引っ掛けのための文字だとか言ってますが、問題文を読む限り、そうは思えませんねぇ。

というわけで、猿が最初にいた高さによって場合分けしないといけないよなぁ……と思いつつ、この問題を解いていくことにしましょう。

……とその前に、問題文で与えられた文字が気に食わないので、問題文の後半を少しいじくります（笑）。

　猿と射手の距離を a とし、最初に猿がいた枝の高さを H 、弾丸が猿のいた木に到達するまでの時間を t 、その時の弾丸の高さを h_i(t) 、その時の猿の高さを h_j(t) 、弾丸の初速度を v 、重力加速度を g とする。尚、空気抵抗は存在しないものとする。

h(i) と書いたとき、 () の中にはその関数内の変数を書かないと、私はどうしても気持ち悪く感じてしまいます。より厳密には変数はイタリック体で書いた方がよいのでしょうが、デザイン的な意味でここではノーマルで表記します。

さて、ここで力学の根本、力学における基礎方程式と言えば？

そう、ニュートンの運動方程式ですね！　ニュートンの力学の第2法則です。

運動方程式より、弾丸の質量を m 、垂直上向きを正として、加速度を a_y とすると、

ma_y = -mg　　……(1)

と表されます。

ここで(1)式より、質量 m は消去され、

a_y = -g　　……(2)

となります。ここで加速度 a_y を積分すると速度 v_y になることから、(2)式の両辺を t で積分して、

v_y = -gt + v_y(0)　（v_y(0) は積分定数）　　……(3)

v_y(0) は、垂直方向の初速度を表します。ここではもちろん0ですから、

v_y = -gt　　……(4)

と(4)式が導出されました。受験物理では、この(4)式は暗記です（爆）から、ここから実際の答案をスタートさせてもよいでしょう。

速度を積分すると移動距離になることから、(4)式の両辺を t で積分して、

h_i(t) = -1/2 gt² + h_i(0)　（h_i(0) は積分定数）　　……(5)

h_i(0) は、弾丸の垂直方向の初期位置を表します。要するに最初の高さ。ここでは H ですから、

h_i(t) = H -1/2 gt²　　……(6)

受験物理では、この(6)式の一般形も暗記です（爆）から、ここから実際の答案をスタートさせてもよいでしょう……かね。

一方、モンキーの質量を M とおいて……とやっていってもいいですが、(1)式→(2)式の段階で、質量は消去されています。ここで(4)式を見ると、「物体はその質量によらず、ピサの斜塔の上から静かに放すと、同じ速度で落下する」というガリレオさんパネェッス、の実験結果が表されるわけですね。てなわけで、猿に対しても、

h_j(t) = H -1/2 gt²　　……(7)

が言えて、

h_i(t) = h_j(t)　　……(8)

が成り立つわけです。

ところで、積分の話はいい……ですよね？　a-t 図における面積が v （⇔v-t 図の傾きがa ）で、v-t 図における面積が x （⇔x-t 図における傾きがv ）です。 x は本問では h ですが。

さてさて、ここで弾丸が猿に衝突する時間を t = t_hit とします。

弾丸は、水平方向には（空気抵抗を無視しているため）何の力も働かず、等速直線運動を行うので、水平方向の速さ v_x は

v_x = v　　……(9)

で一定。よって、弾丸が猿に衝突するまでの時間は、

t_hit = a/v　　……(10)

(6)式に(10)式を代入して、衝突時の弾丸（と猿）の地面からの高さは、

h_i(t_hit) = H -1/2 g t_hit²
　　　　 = H -1/2 g (a/v)²　　……(11)

この高さが0以上のとき、すなわち h_i(t_hit) ≧ 0 のとき、モンキーが地面に着く前に弾丸がモンキーハンティングする。これすなわち、

H -1/2 g (a/v)² ≧ 0
　　　　　　　 ∴H ≧ 1/2 g (a/v)²　　……(12)

のときなり。

衝突時の高さが0未満、すなわち h_i(t_hit) ＜ 0 のとき、猿ははね返ったり、地面にめり込んだりすると面倒くさいので丁重に無視して、猿が自分から地面を駆けて弾丸に当たりにいかない限りは、弾丸は猿に衝突しない。

以上より、

H ≧ 1/2 g・(a/v)² のとき、弾丸は猿に衝突する。
H ＜ 1/2 g・(a/v)² のとき、猿は弾丸に衝突される前に地面に着いてしまい、その場に猿が留まったとすると、弾丸は猿の頭上を通過する。

という答えが得られるわけですね。

＜モンキーハンティング＞

一方、一般的なモンキーハンティングの問題は、ハンターは地面から木の上の猿を狙います。弾丸の発射と同時に猿も木から落ちる状態になって、猿が自由落下し始めるとすると、ハンターは銃から弾丸をどれくらいの初速度で、どの角度へ打ち出せばいいか、というのが一般的なモンキーハンティングの問題です。

ここで図に示した文字の他に、弾丸の高さを h_bullet(t)、猿の高さを h_monkey(t)、弾丸が猿に衝突する時間を t_hit とし、木の高さが十分に高い（笑）とすると、

t_hit = a/v_x　　（∵(10)式）　　……(13)
v_y(t) = v_y(0) - gt　　（∵(3)式）　　……(14)
h_bullet(t) = v_y(0) t - 1/2 gt²　　（∵(14)式をtで積分、弾丸の最初の高さは h=0 ）　　……(15)
h_monkey(t) = H -1/2 gt²　　（∵(7)式）　　……(16)

t = t_hit において、(15)式・(16)式より、

v_y(0) t_hit - 1/2 gt_hit² = H -1/2 gt_hit²

よって、

∴v_y(0) t_hit = H　　……(17)

ここで、

v_y(0) = v(0) sinθ　　……(18)
v_x = v(0) cosθ　　……(19)

であるから、(17)式より、

H = v(0) sinθ ・ t_hit　←(18)式代入
　 = v(0) sinθ ・ a/v_x　←(13)式代入
　 = v(0) sinθ ・ a/ (v(0) cosθ)　←(19)式代入
　 = a tanθ　　……(20)

ゆえに、弾丸の初速度は消去され、モンキーハンティングに必要な条件は、

tanθ= H/a　　……(21)

の角度の条件のみとなります。θ= Arctan(H/a)。

tanθ= H/a とはすなわち、弾丸を発射する際、銃口は猿に向けて発射せよ、ということです。

すなわち、「モンキーハンティング」においては、ハンターがいる位置（高さ）や弾丸の初速度には関わりなく、とにかく照準を猿に合わせて弾丸を撃てば猿を仕留めることができる、というわけです。もちろん、猿が着地するよりも早く水平方向で弾丸がサルに追いつく、また空気抵抗が無視できる場合に限りますが。

では、冒頭のバカテストはどうだったでしょうか？　モンキーハンティングにおけるθ＝０の場合ですね。サルと同じ高さから銃を撃っています。そして、ちゃんとサルに銃口を向けて弾丸を射出しているため、サルに弾丸を衝突させることができる、というわけです。

＜結論＞

恋の弾丸は相手に向けてまっすぐに撃ち込むべし。

「バカテスト一覧」に戻る

＜出典＞