バカテスト・数学

（ライトノベル『バカとテストと召喚獣』（第1巻） pp.60-61）

第４問

問　以下の問いに答えなさい。 

 (1） 4sinX + 3cos3X = 2 の方程式を満たし、かつ第一象限に存在するXの値を一つ答えなさい。

 (2） sin(A+B) と等しい式を示すのは次のどれか、�@〜�Cの中から選びなさい。

�@ sinA + cosB	�A sinA - cosB
�B sinAcosB	�C sinAcosB + cosAsinB

　　　


＜姫路瑞希の答え（模範解答）＞
 （1） X = π/ 6
 （2） �C



＜解説＞

（1）
第一象限に存在するXの値を一つだけ答えればいい、という
（京大数学でよく見かける）十分条件系の問題（もちろん、問題のレベルは全く違うが…）なので、
まあ、あてずっぽうにXの値を代入して、それが成立すればOK。

答案用紙には、

　（1）　X = π/6 （ は題意を満たす。）

とでも書けば、そりゃもう、非の打ちどころのない完璧な答案です。
（もちろん、こんなアホな問題は普通は出題されない。）


まあ、しかし、あてずっぽうに代入していくのも、なんだか灼……じゃなくて癪なので、
ここでは、グラフを利用して求めてみることにしましょう。

　　4sinX + 3cos3X = 2
の解は、

　　Y = 4sinX + 3cos3X
と
　　Y = 2
の交点のX座標と考えることができます。

所謂「定数分離（パラメータ分離）」の手法と途中まで似た感じで解いていくわけです。

定数（パラメータ）を分離し、グラフを利用して定数の値の範囲を求める、超有名な必須手法ですから、
知らない人はいないでしょう。

万が一知らないのであれば、Dクラスに戻って出直してくること！


さてさて、
まあ、Y=2 のグラフが描けない人はいませんから、

問題は、
　　Y = 4sinX + 3cos3X
のグラフをどう描くかです。

X=π/12、π/6、π/4、…と有名角を代入して、点をプロットしていくか…？
それじゃ、結局最初の式にあてずっぽうに代入していくのと変わりありませんし、面倒くさいな…。


というわけで、
　　Y = 4sinX
と
　　Y = 3cos3X
のグラフを足し合わせるという方法を使うことにしましょう。

まず、
　　Y = 4sinX
と
　　Y = 3cos3X
のグラフを描きます。

まさかとは思いますが、この2つのグラフが描けない人はいませんね？

万が一、そのような人がいるのなら、Fクラスに戻って出直してきなさい！


そんなわけで、グラフは下図。


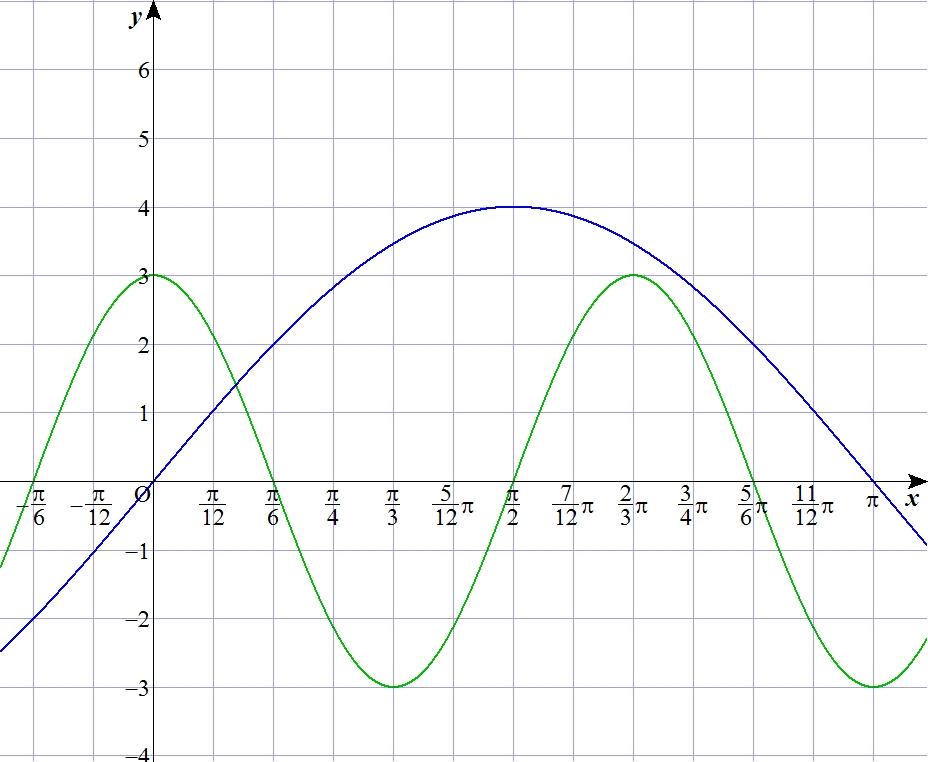
（関数グラフソフトGRAPESを利用）


Y = 4sinX のグラフは、Y = sinX のグラフを縦（Y軸方向）に4倍拡大したものであり、

Y = 3cos3X のグラフは、Y = cosX のグラフを縦（Y軸方向）に3倍拡大し、横（X軸方向）に1/3倍拡大したものです。
周期が2π/3になってるのがポイント。


以上のようなことは、ちゃんと数II の三角関数（かな？）で勉強しましたね？

…あれ？　でも数II の三角関数ってことは、普通は高2で習うのだろうか…？

まあ文月学園は進学校ですから、ちょっと進路は早い…というか、おそらくクラス間格差が激しいんでしょう。

しかしまあ、電子黒板っつうやつは、なかなかよさそうです。

「黒板」だと、前の方の席にいると、どうもチョークの粉をよく吸いこんでる気がして、
アスベストのように、肺気腫になったり、気管支炎になったりするんじゃないかとちょっと心配ですね。


＜↑追記＞
チョークの主成分が、炭酸カルシウム、または硫酸カルシウムであることを考慮すると、

炭酸カルシウム（CaCO₃）なら、炭酸の電離等々を全部まとめて書けば、

　　CaCO₃ + CO₂ + H₂O → Ca(HCO₃)₂

の反応により、炭酸水素カルシウムとなって溶けてしまいますし、


硫酸カルシウム（CaSO₄）でも、水に難溶、とは習いますが、
実は、1Lの水に2gぐらいは溶けてしまうので、
チョークの粉程度なら、十分血液中に溶けてしまいますね。


以上から考察するに、チョークを食べるという暴挙に出ない限りは、
まあ多少ならチョークの粉を吸い込んでも大丈夫でしょう。



　*　*　*　*　*

えっと…、では次に、この2つのグラフを足し合わせませてみましょう。

ここでもしも、グラフの足し算（グラフの重ね合わせ）ができない人がいましたら、
Eクラスに戻って出直してきてくださいっ！！

私も暇じゃないんですよ…！？









……えっ、ホントに行っちゃうんですか？


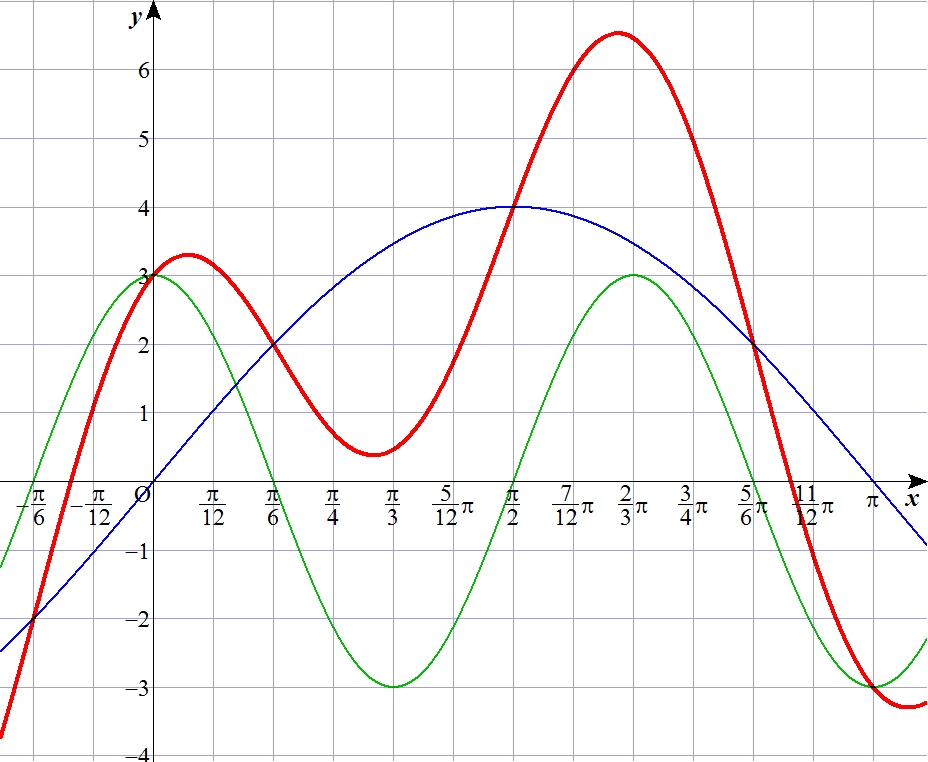
Y = 4sinX
Y = 3cos3X
Y = 4sinX + 3cos3X




いいですか？　ポイントは、足し合わせる青と緑のグラフの、どちらかのY座標が0になる点、
そして、2つのグラフが交わる点です。

どちらかが0になれば、足し合わせたグラフは、当然もう一方のグラフの点を通るはずです。

そして、2つのグラフが交わるところでは、そのY座標を2倍した点を、足し合わせたグラフは通るはずですね？

そしてそれらの点のプロットが終わったら、後は勘とセンスと経験値の問題です。
うまくつなぎ合わせてくださいっ。



　*　*　*　*　*

はてさて、ではY = 4sinX + 3cos3X のグラフも描けたことですし、Y=2 のグラフとの交点を第一象限において考えてみましょう。

第一象限とは？

もちろん、0 < X < π/2 の範囲のことですね。
（座標平面において、X>0 かつ Y>0 の領域のこと。一応、X軸、Y軸は含まないことになっている）



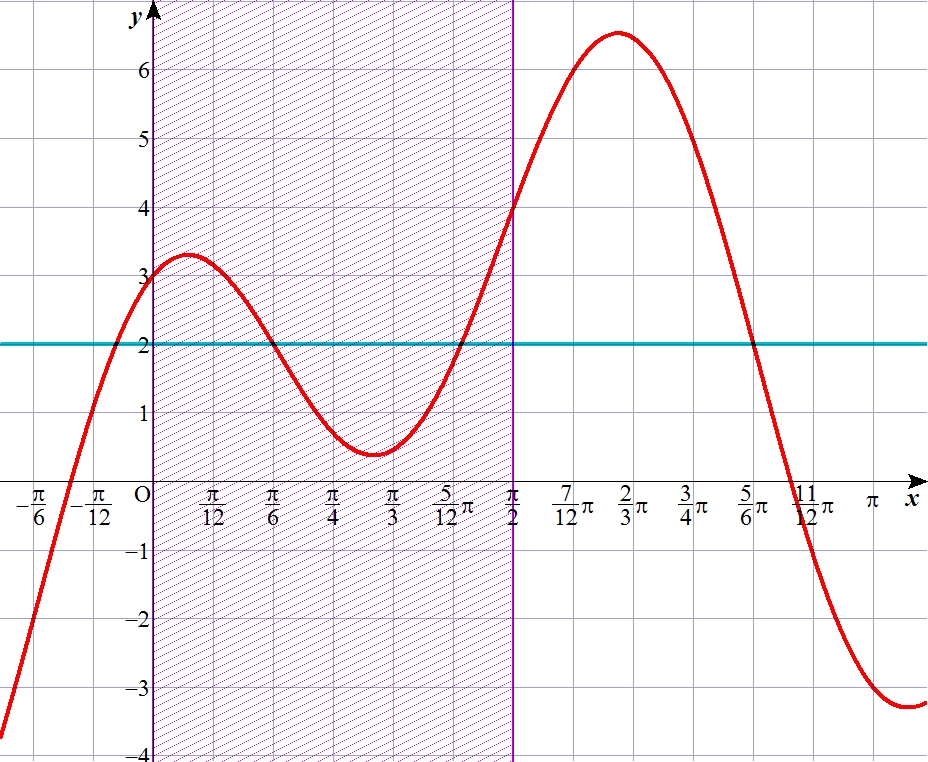
さあ、上手にグラフが描けると、X=π/6、5π/12 あたりに解がありそうなことが分かります。

さあ、代入してみましょう。

X = π/6 を代入。

Y = 4sin（π/6） + 3cos（3π/6） =　4・1/2 + 3・0 = 2

成立！


X = 5π/12 を代入。

Y = 4sin（5π/12） + 3cos（15π/12） = 4・（√6 + √2)/4 - 3・1/√2 = （2√6 - √2）/2 ≒ （2・2.4 - 1.4） /2 = 1.7

不成立…。

まあ、√が大量発生した時点で怪しいですけどね。

ん…？
sin75°？

sin15°= ( √6 - √2 ) /2
cos15°= ( √6 + √2 ) /2

を覚えておけば、導き出せるのじゃ。

覚えるに足る有名式だと思うがの。


そんなわけで、75°がダメだったので、（90°は第一象限ではない！）
これより大きい角度は、一介の高2には代入できませんっ！

sin80°の近似値を知ってるゼ！　とかいうのは、もはや変態です。




　*　*　*　*　*

そういうわけで、本気で求めようと思うと、やはり裏技では無理なのです。

三角関数らしい解き方をしなければなりませんね。


さあ、『バカとテストと召喚獣』を読んだ、大概の読者の方々は、あの問題を見た瞬間、ああ、「三倍角の公式」 だと！

しかし、三倍角の公式を使って解いていくと、異常に面倒くさい目にあいます…（汗）。



では、真面目に三角公式を使って解いていくことにしましょう。

なお、Xの範囲は、0≦X＜2πとして以下解いていきます。

それが、普通の問題ですからね。


　　4sinX + 3cos3X = 2　―― {1}
⇔ 4sinX + 3 ( -3cosX + 4cos³X ) = 2　（←三倍角の公式　cos3X = -3cosX + 4cos³ X を利用）


ここで、cosX = m （-1≦m≦1）とおくと、 sinX = ±√（1-cos²X） =±√（1-m²）となり面倒ですね…

というわけで、あらかじめ {1}式 を2乗しておくことにしましょう。


さて、cos3X って何かイヤですよね？
イヤなやつからはみんな逃げていきます。

　　3cos3X = 2 - 4sinX　（4sinX が右辺に逃げる）

2乗して、
　　9cos²3X = 4 - 16sinX + 16sin²X　―― {2}


ここで、cosX = m （-1≦m≦1）とおくと、 やはり、sinX = ±√（1-m²）となり面倒なので、
sinX = t （-1≦t≦1）とおくのが得策でしょう。


すると、{2}式は、
　　9cos²3X = 4 - 16t + 16ｔ²　　―― {3}
となり、

ここで、
　　cos²3X = 1 - sin²3X　　（∵ sin²3X + cos²3X = 1 ）
　　　　　　　= 1 - （3sinX - 4sin³X）²　　（∵ sin3X = 3sinX - 4sin³X ）
　　　　　　　= 1 - （3t - 4t³ ）²
　　　　　　　= 1 - （9t² - 24t⁴ + 16t⁶ ）
　　　　　　　= -16t⁶ + 24t⁴ - 9t² +1


{3}式に代入して、
　　9 ( -16t⁶ + 24t⁴ - 9t² +1 ) = 16t² - 16t + 4
整理して、
　　 144t⁶ - 216t⁴ + 97t² - 16ｔ - 5 = 0

となり、6次方程式を解くことになります！！

頑張って変形すると、
　　（t-1/2)² （144t⁴ + 144t³ - 108t² - 144ｔ - 20 ） = 0

となります。

　　t = 1/2
⇔ sinX = 1/2
⇔ X = π/6、5π/6
となりますね。

第一象限の解は、X = π/6 ということになります。


一方、
　　 144t⁴ + 144t³ - 108t² - 144ｔ - 20 = 0

は、もう高校生には解けません…。



結局、下図の


5π/12 よりも少し大きい解は、高校生には求めることができません…。


パソコンの手を借りるしかなさそう ですね…。



というわけで、「Wolfram|Alpha」の力を借りましょう。

するとその解は、

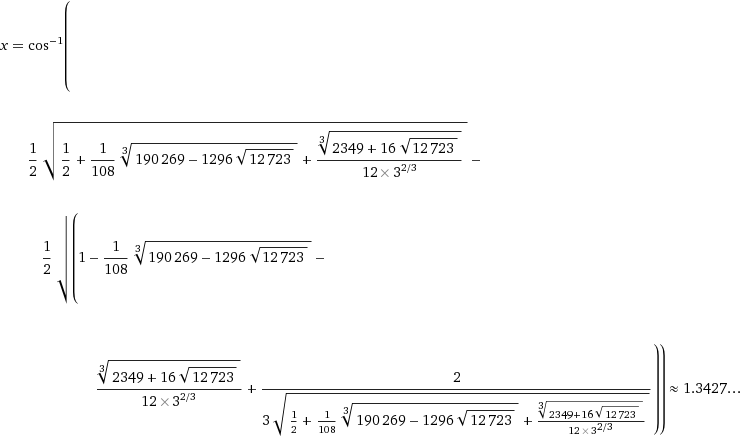
…ということで（笑）。

しかしまあ、よくぞここまで計算してくれました。



要は、適当に有名角を代入していく方が早いという、とんでもない悪問だったわけです。

まあ、「始めに答えありき」な問題だったんでしょうね…。


まず、答えを　X = π/6 にしよう、と決めて、テキトーに式を作ったのでしょう。

特に、
　　4sin（π/6） + 3cos（3π/6） =　4・1/2 + 3・0 = 2
　　　　　　　　　ココ（↑）が0になるトコロが怪しい…。


そして、グラフを描いてみたところ、何か、X = π/6 以外の余計な解ができてしまったばっかりに、

「第一象限に存在するXの値を 一つ 求めなさい」という変な問題にしたんじゃないでしょうかね？





（2）
　（1）の記事があまりにも長くなって、（2）の問題を忘れた人のためにもう一度問題を。

 (2） sin(A+B) と等しい式を示すのは次のどれか、�@〜�Cの中から選びなさい。

�@ sinA + cosB	�A sinA - cosB
�B sinAcosB	�C sinAcosB + cosAsinB

　　　

そりゃ、�Cだろ！！　（←Mac派の人にも丸数字が見えるようにしたつもりですが、もし表示されてなかった連絡をば）


「コスモス公式」か何かの語呂合わせで、ちゃんと暗記してますね。

おそらく授業でちゃんと証明法は習ったことでしょうが、もう完璧に忘れてしまっているはずです（笑）。



そんな基礎を踏み固めていない受験生に警鐘を鳴らすために、東大が課した問題が、次の有名な問題です。

1999年の東大前期、数学の第1問（文理共通）に登場した問題ですね。

その問題は以下の通りです。

（1）　一般角θに対してsinθ、cosθの定義を述べよ。 （2）　（1）で述べた定義にもとづき、一般角α、βに対して 　　　　　sin（α+β） = sinαcosβ + cosαsinβ、 　　　　　ｃｏｓ（α+β） = cosαcosβ - sinαsinβ 　　を証明せよ。

駿台と代ゼミは最近の2ヶ年分しかネットでは公開していないので、
参考として河合塾の答え にリンクを貼っておきます。


河合塾は、一般的な教科書に書いてあるように、「距離の公式」 を用いて証明していますね。

他に、ベクトル を利用して解くという方法もあります。


ただし、オイラーの公式から三角関数の加法定理を証明しようとすると、循環論法となり、大減点 を食らうそうで。

その理由は、教科書におけるオイラーの公式の証明に、三角関数の加法定理が用いられているから、ということですが、

2009年現在では、オイラーの公式、および複素数平面などの一部の複素数分野は、指導要領外となっており、
高校の教科書にはそもそも、オイラーの公式などというものは載っていません ね（爆）



が、2012年度からは、学習指導要領が改訂されて、「複素数平面」 とかが復活するとか。

で、また「行列」 は消滅するようです…。

というか、「数学C」 自体が消えてなくなると。


主な変更点はブログにまとめてみました。だいたい次のような感じです。




＜結論＞

せめて、まともな計算で解ける問題にして！
代入して答えが出ちゃう裏技なんて、センター試験だけで十分だよ！

「バカテスト一覧」に戻る

＜出典＞

　

バカとテストと召喚獣 (ファミ通文庫)
井上 堅二
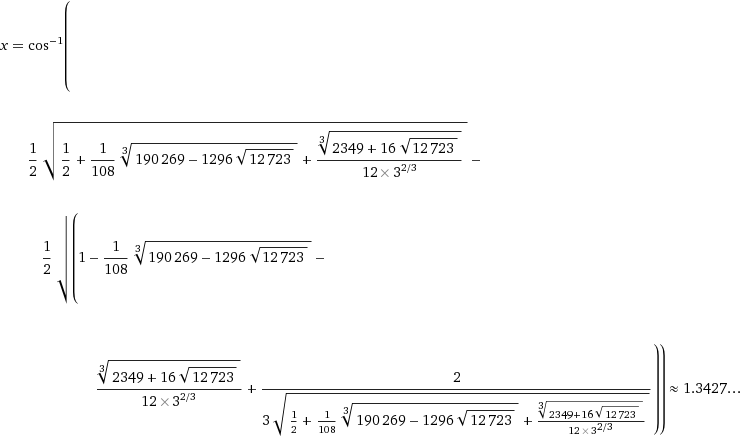