|
かの浸透圧に関する法則、「ファントホッフの法則」を発見したのが、オランダの化学者である
ヤコブス・ヘンリクス・ファント・ホッフです。
ファントホッフは、特に物理化学の分野で多くの功績をあげており、
1886年に、「希薄溶液の浸透圧は、溶質の濃度と絶対温度に比例する」というファントホッフの法則を発見し、
その15年後にあたる1901年に最初のノーベル化学賞を受賞しました。
さて、ファントホッフの式というものは、実はいくつもあるのですが、
中でも一番見慣れたものは、
ΠV=nRT
でしょう。ΔrH
°が登場する方が見慣れている方もいらっしゃるかもしれませんが。
さて、このΠV=nRTですが、
Π[Pa]は希薄溶液の浸透圧、
V[L]は溶液の体積、
n[mol]は溶質の物質量、
T[K]は絶対温度、
そして、注目の比例定数Rは、8.3×108、つまり気体定数と等しいわけで、
理想気体(完全気体)の状態方程式 PV=nRT
と同じ関係式となるわけですが、
なぜ浸透圧にも同じ関係式が成立するのか、というと、
ファントホッフは「溶液の浸透圧とは、溶液中からすべての溶媒分子を取り除いたと仮定したとき、
溶質粒子の自由な運動によって引き起こされる圧力である」と考えたからなんですね。
つまり、気体分子が熱運動によりできるだけ広い空間を占めようとして、容器の壁に衝突し、
温度と粒子数(物質量)で決まる一定の圧力Pを作りだすのと同じように、
半透膜によって遮られた空間内に存在する溶質粒子も、できるだけ広い空間を占めようとして膜に衝突し、
この動きが原因となり、半透膜の細孔から溶媒分子が浸入して、浸透圧Πが生み出される、というわけです。
(『どこぞの怪しい?参考書 』のp.157より) 』のp.157より)
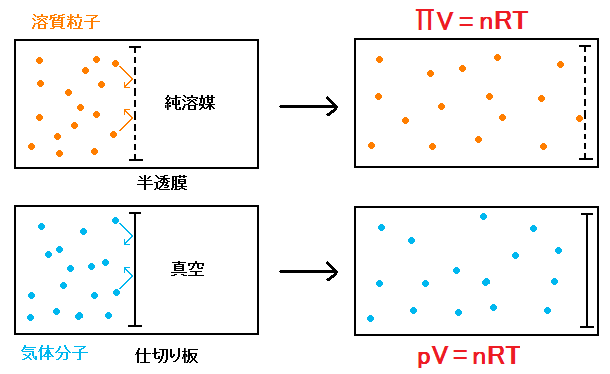
さあ、上の図を見てください。
ほら、(希薄溶液の)浸透圧も、(理想気体の)気体の圧力も同じようなものではないですか!
さて、難しい話はここまでにして、
この浸透という現象がどのような場所で使われているのかを見ていきましょう。
…という話をする前に注意をば。
「浸透」と「透析」は別物です。
私も以前勘違いしておりました。
医療分野でよく耳にする人工透析などの「透析」とは、溶質が移動する場合のことを指します。
一方で、「浸透」は、溶媒が移動する場合ですよね。
さて、身近な「浸透」の現象といえば、
漬け物
青菜に塩
ナメクジに塩(爆)
梅酒
などですかね。
前の3つはいいとして、梅酒のどこに浸透の原理が導入されているのかというと、
梅酒を作る際には、梅の実を氷砂糖の入った焼酎の中に漬けておきますが、
最初は梅の実の内部の濃度の法が大きく、外部からどんどんアルコールが入ってきて梅の実が膨らみます。
そして、入ってきたアルコールに梅の味や香りが十分に溶けこむ一方で、
外部では、着々と氷砂糖が溶け出し、アルコール溶液中の砂糖の濃度が高まっていきます。
すると、今度は、梅の味や香りが十分に溶け込んだアルコールが梅の実の内部から外へと出て行くわけですね。
だから、梅酒作りに粉の砂糖は使えない、というわけなのでした。
昔の人の知恵というものは、本当にすごいものですね。
さて、この「浸透」の現象を応用した「逆浸透」という方法があります。
溶液側に浸透圧より大きな圧力を加えることによって、溶媒を純溶媒側へと流し込む手法です。
この方法は、海水を淡水化するための方法として極めて重要な方法で、
これを利用して飲料水や灌漑用水をつくるための施設、逆浸透プラント(海水淡水化プラント)
が世界中で稼働しています。
日本最大のプラントは、福岡市東区にあるもので、淡水供給量は5万トン/日です。
日本は、海水淡水化用の逆浸透膜の生産に関しては、世界でもトップクラスであり、
さらなる技術の発展が期待されています。
これからの将来を担っていく私たちの責務は大きいですね。
これとは他に、ファントホッフが提唱した、高校化学でもおなじみの理論といえば、
炭素原子の正四面体構造説
です。
すなわち、もし炭素の4つの原子価が平面上で互いに直角をなすとすると仮定するならば、
発見されているよりもはるかに多くの異性体が予測されるけれども、
もし原子価が四面体の方向を向いているとすれば、この問題は解決される、というわけです。
たとえば、CR1R2R3R4
という分子の異性体は、
正四面体構造説によれば、下図の赤四角で囲った2つだけですが、
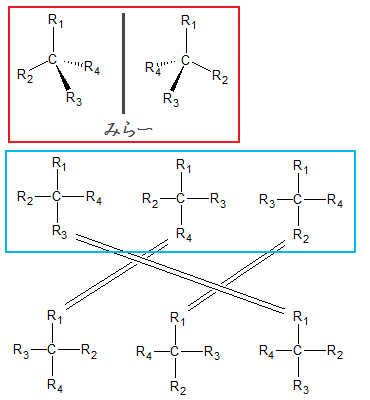
もしも、全原子が平面上に固定されているとすると、何種類の異性体が存在することになるかな?
という数学の問題になります(笑)
円順列の応用版、いわゆる、数珠順列の問題です。
R1を上に固定して、のこり3つを並べると考え、3!= 6
通りとしたくなるところですが、
裏返せば同じになるものが存在しますから、2で割って、3通りとなりますね。
私は場合の数、確率が大の苦手なので、説明に不備があっても私のせいではありません。(責任逃れ)
さらに、ファントホッフは、
シス-トランスの異性体に関して、マレイン酸とフマル酸の異性体の存在も解明しました。
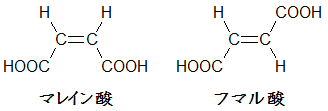
(HOOC-はおかしいんじゃないの?という異議申し立ては認めませんw)
なお、「シス」「トランス」の用語は、バイヤーが1892年に導入したものです。
今日の有機化学の基礎となる立体化学の土台を築いたのは、(教科書に直接名前は登場しませんが、)
他ならぬ、ファントホッフだったのです!
|