フロン(A)とメタン(D) ですね。
フロンはオゾン層の破壊だけでなく、地球温暖化も引き起こしているのです。
京都議定書において削減対象となっている温室効果ガスは、
二酸化炭素(CO2)、メタン(CH4)、一酸化二窒素(N2O)、代替フロン、六フッ化硫黄(SF6)です。
他に温室効果ガスとしては、水蒸気(H2O) なんかも有名ですね。
イ オゾン(O3)は酸素の同素体で、酸素中で無声放電を行うか、酸素に強い紫外線(G)を当てると生成します。
成層圏において、オゾンは主に3200Å以下の紫外線を吸収して分解し、もとの酸素分子に戻ります。
この反応によって、生物にとって有害な3200Å以下の紫外線が地表に届くのを防いでいるのです。
ところが、近年、フロン(A)の分解によって生じる塩素ラジカル(K)により、
オゾン層の破壊が起きています。
フロンは、正式には、クロロフルオロカーボン(クロロ=Cl、フルオロ=F、カーボン=C)と呼ばれ、
炭化水素の水素をフッ素や塩素で置換した化合物の総称です。
フロンは化学的に非常に安定で、容易に分解せず、約10年かかって成層圏まで拡散していきます。
フロンは成層圏で強い太陽の紫外線を受けて分解し、塩素ラジカル(Cl・)を生じます。
塩素ラジカルとは、不対電子を持つ原子、要するに、塩素原子そのものです。
この塩素ラジカルがオゾンをぶっ壊していくわけですが、
厄介なことに、この塩素ラジカルは、オゾンを分解しながら、自らも再生するのです。
Cl・ + O3 → ClO・ + O2
ClO・ + O・ → Cl・ + O2
この辺の詳しい反応については、化学グランプリ2006年度の第1問の問題にあるので、
そちらを参照してください。(いい加減な48K部長であった。)
ウ 酸性雨の原因と言えば、ソックス、ノックスですね。
つまり、硫黄酸化物(SOx)、窒素酸化物(NOx)(H)です。
これらは、地上到達前の雨水と酸素と反応して、
それぞれ硫酸(H2SO4)と硝酸(HNO3)(N)を生じます。
私たちは、雨の日には、希硫酸と希硝酸の溶液を被ってるわけなんですね。
そりゃ、ブロンズ像だって溶けてまうわ。
|
問2 (ア) 室温(20 ℃)での、1mol の液体の水(H2O)の体積は、
原子量として、H = 1.0 、 O = 16 が与えられているので、
18g と分かりますね。
ここで、水の密度は室温付近では、ほぼ 1g = 1cm3 なので、
その 1mol の液体の水の体積は、18g = 18cm3 = 18mL となります。
有効数字2桁で答えてますね。
(イ) 室温(20 ℃)、1 気圧での、1mol の気体の水(H2O)の体積は、
273 K, 1.013×105 Pa (= 1 atm)での気体 1 mol の体積 = 22.4 L
という条件が与えられているので、22.4L。
有効数字2桁なので、22L …というのは間違いですね。
そうです! 温度の条件を無視していますね。
圧力一定のもとで、気体の体積V は絶対温度T に比例する。
V ∝ T
V1/T1 = V2/T2
という、シャルルの法則を適用しましょう!
室温 20℃(= 293K)での体積をV2とすると、
22.4 / 273 = V2 / 293
∴ V2 = 24.04… ≒ 24(L) となります。
(ウ) 1mol あたり、液体は18mL、気体は24L(= 24000mL)。
つまり、気体状態での密度の方が、1000(=103)倍大きい、
すなわち、3桁程度大きいのです。
問3 物理、特に力学の問題ですね。
力学においては、まず、物体に働く力を書きだすのが基本です!
では、図1に書き込んでみましょう!
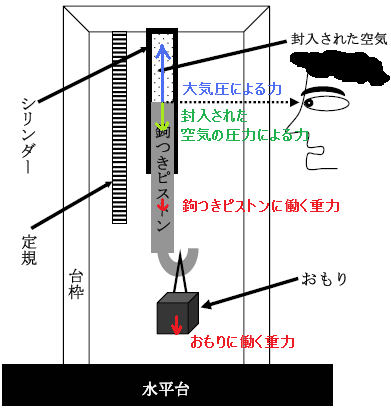
その上で注目するのは、封入された空気と鉤つきピストンとの境界面ですね。
| |
← このような図で表せますね。 青字は、大気圧による力。 緑字は、封入された空気の圧力による力。 赤字は、鉤付きピストンとおもりに働く重力の和です。 おもりに働く重力が、作用線上からズレてますが、あまり気になさらないよう。 |
さて、そもそも、圧力とは、単位面積当たりに働く力のことですから、
P[Pa] = F[N] / S[m2] で表せます。
ですから、F[N] = P[Pa]× S[m2]
となります。
求めたい封入された空気の圧力をP200[Pa]とおくと、
大気圧による力は、1.00×105(Pa)×1.00×10-4(m2) = 10.0[N]
封入された空気の圧力による力は、P200[Pa]×1.00×10-4(m2) = 1.00×10-4×P200[N]
鉤付きピストンとおもりに働く重力の和は、(100+200)×10-3(kg)×9.81(m s-2) = 2.943(N)
∴ 力のつりあいの式より、
10.0 = 1.00×10-4×P200 + 2.943
これを解くと、P200 = 70570 (Pa)となります。
これを有効数字3桁にして、7.06×104 Pa、これが答えです。
<別解> 圧力のつりあいの式を作って解きます。
| |
青字は、大気圧。 緑字は、封入された空気の圧力。 赤字は、鉤付きピストンとおもりに働く重力の和による圧力。 のように考えて解く方法です。 |
求めたい封入された空気の圧力をP200[Pa]とおくと、
大気圧は、1.00×105[Pa]
封入された空気の圧力による力は、P200[Pa]
鉤付きピストンとおもりに働く重力の和による圧力は、
(100+200)×10-3(kg)×9.81(m s-2) / 1.00×10-4(m2) = 29430(Pa)
∴ 圧力のつりあいの式より、
1.00×105 = P200 + 29430
これを解くと、やはり、P200 = 70570 (Pa)となります。(そりゃそうですが)
これを有効数字3桁にして、7.06×104 Pa、これが答えです。
こちらの方が、若干計算は簡単に済みます。
問4 おもりを400g にした場合の封入された空気の圧力も同様に求めます。
今回は、圧力のつりあいの式から解いてみます。
求めたい封入された空気の圧力をP400[Pa]とおくと、
大気圧は、1.00×105[Pa]
封入された空気の圧力による力は、P400[Pa]
鉤付きピストンとおもりに働く重力の和による圧力は、
(100+400)×10-3(kg)×9.81(m s-2) / 1.00×10-4(m2) = 49050(Pa)
∴ 圧力のつりあいの式より、
1.00×105 = P400 + 49050
これを解くと、P400 = 50950 (Pa)となります。
とりあえず有効数字3桁にすると、5.10×104 Paになります。
そして、PとVの関係を調べます。
|
おもりの重さ |
P[Pa] |
V[cm3] |
|
200g |
7.06×104 |
1.50×101 |
|
400g |
5.10×104 |
2.08×101 |
せっかく、選択肢が与えられているので、実際に計算してみた方が早いでしょうね。
電卓もあることですし。(化学グランプリに参加すると、無料で電卓が貰えます!)
以降、電卓が貰えるぜ! ということを別の大問でも繰り返すことがございますが、ご了承ください。
さて、計算してみますと、
|
おもりの重さ |
P[Pa] |
V[cm3] |
PV |
P/V |
V/P |
P+V |
|
200g |
7.06×104 |
1.50×101 |
1.059×106 |
4.706×103 |
2.124×10-4 |
7.061×104 |
|
400g |
5.10×104 |
2.08×101 |
1.060×106 |
2.451×103 |
4.078×10-4 |
5.102×104 |
(※小数第4位切り捨て)
最初のPVを計算した時点で、もう答えが出ましたね。
答えを最初に配置してくれるなんて、なんて親切なんでしょう!
というわけで、答えは、PV(ア)です。
(b)は、単位もつけ、有効数字3桁で、1.06×106 Pa cm3
俺はセンチなんて許さないゼ! という人は、
1m3 = 1000000 cm3 = 106 cm3 より、
1.06 Pa m3 としてもよいでしょう。
ところで、[Pa] = [N/m2] と表すことができましたね!
ということは、[Pa⋅m3]=[N⋅m3/m2]=[N⋅m]となります。
よって、 1.06 N m と表すこともできます!
そして、さらにさらに、
[N]=[kg⋅m/s2] と変換することができます!
ということは、[N⋅m]=[kg⋅m⋅m/s2]=[kg⋅m2/s2]となりますので、
よって、 1.06 kg m2 s-2 とするのもOKでしょう。
徹底的に分解されましたね。
さてさて、そもそも、この 温度一定の条件でPVが一定になる という結論、
かの ボイルの法則 のことだったんですね!
|
|
|
|