|
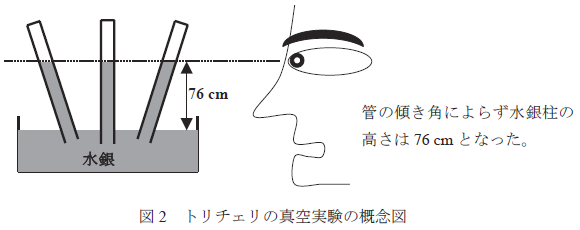
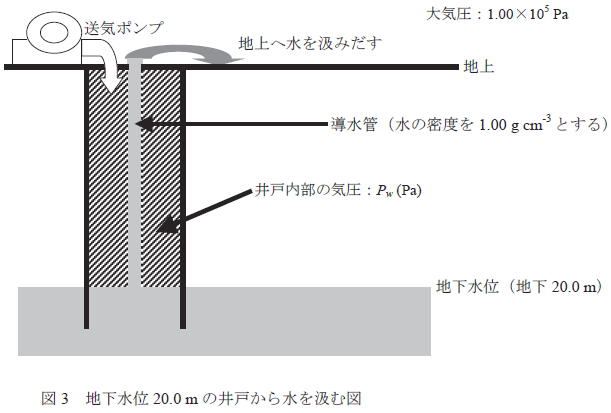
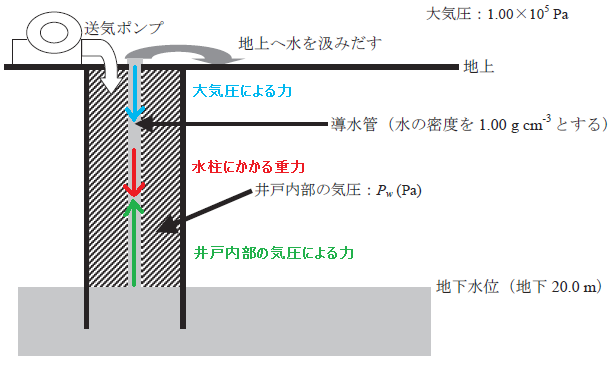
さて,前問で「圧力」について扱ったが,この圧力は,自然科学,環境,工業,日常生活のあらゆる場面で出会うひとつの重要な「状態の指標」である。以下,この圧力にまつわるいくつかの問題をさらに掘り下げて考えてみよう。 先ず日常的な例から考えてみよう。手こぎの井戸のポンプが昔からあるように,地下水を地上へ汲み(くみ)上げる際には汲み上げポンプを使う。しかし地下水を引っぱり上げるだけの方式の汲み上げポンプでは,水位が地下10 m 以上の深さの地下水は汲み上げられないことが知られている。また,例えば15 m の高さの台に登って台上で汲み上げポンプを用いて地上から水を汲み上げようとしても,水は地上から約10 m までしか上がらない。すなわち,汲み上げポンプでは水面からある一定の高さ(約10 m)にまでしか水を上げることができない。 これと深く関連した実験は,17 世紀にガリレイの弟子のトリチェリにより行われた(トリチェリの真空実験)。一方の端を密閉した充分に長いガラス管内に液体である水銀を隙間無く満たし,他方の開いた端を水銀の中に保ったままガラス管を倒立させた。このとき,管内に閉じ込められた水銀の高さは管の傾斜角度によらずほぼ76 cm だった。これよりも上には水銀が存在しない「空 (から)」の空間ができる。図2 にこの様子を図式的に示す。 上記の二つの現象は,外気が液面をおす力(大気圧)に相当する分だけ,汲み上げ管内やガラ ス管内に閉じ込められた液体が,液面から上へ上昇することを意味する。上記のトリチェリの真空実験の場合,日によって大気圧が若干上下するため多少のばらつきはあるものの,水銀が概ね760 mm 上昇するので,その高さをもって圧力を表すことができ,「大気圧(≒ 1 気圧)は概ね760 mmHg である」と表現する。もちろん水の上昇の高さでも同様のことを考えることができ,この場合の単位はmmH2O と表記される。 |
|
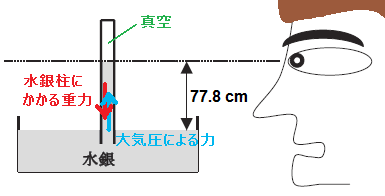
| 問5 水銀柱の高さで表したある日の大気圧が778 mmHg であったとする。これを近年共通使用が推奨されている圧力の単位Pa へ変換し,有効数字3桁で答えなさい。 ただし,水銀の密度は13.6 g cm-3,重力加速度g は9.81 m s-2 であるとし,計算では問題中で与えた値を使い,計算式も示しなさい。 |