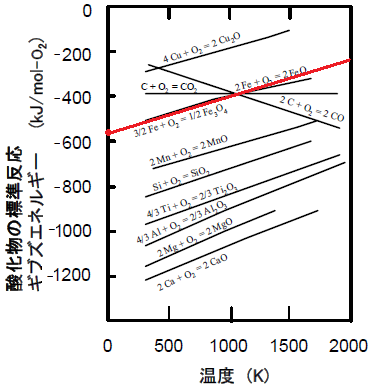
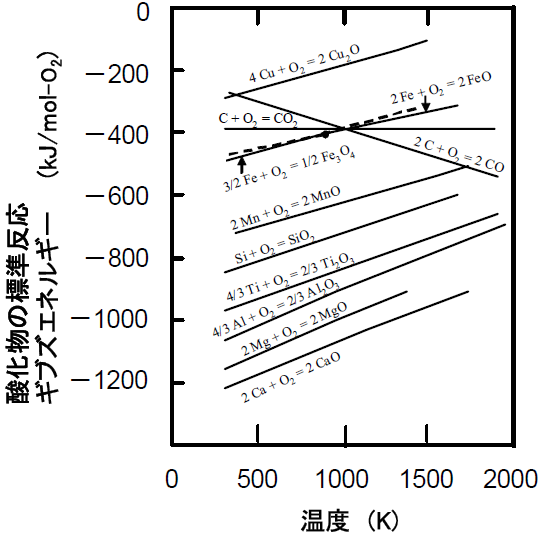
身の回りに存在する金属のほとんどは，地球上では金属としてではなく酸化物などの化合物として存在している。金属の酸化物から金属を取り出すプロセスを金属製錬といい，酸化物の還元にはコークス（炭素）が用いられることが多い。金属M が酸化物 MmOn（m, n は整数） を生成する反応は，1 モルのO2(g) 当たりで表せば，次のようになる。 　　　　2m/n M + O2 → 2/n MmOn　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (10) この反応の標準反応ギブズエネルギーΔGｒ°は絶対温度に対してほぼ直線的に変化し，様々な物質について絶対温度とΔGｒ°の関係を示した図はエリンガム図と呼ばれる。 図１ 各種物質の酸化反応における標準反応ギブズエネルギー−温度線図（エリンガム図）   問７　1000 K においてSi とCu の O2(g) 1 モルとの酸化反応を比較した場合，ΔGｒ°の値から判 　断して，どちらの元素の方が酸化されやすいか答えなさい。また，それぞれの反応の1 bar にお 　けるO2(g) 1 モル当たりの発熱量（反応熱）を有効数字 2桁で求めなさい。

問7　もうギブズエネルギーにも慣れてきましたね。

反応はギブズエネルギーが減少する向きに起こりやすい
＝　標準反応ギブズエネルギーの小さい反応ほど起こりやすい

ということです。

つまり、今回は酸素との反応ですから、
酸化物の標準反応ギブズエネルギーが小さいほど、酸化されやすいということを表しています。


まあ、ここまで深く考えなくても、常識的に、
カルシウムと銅ではどちらが酸化されやすいだろうか、と問えば、
自ずと、エリンガム図で下に行くほど酸化されやすいんだろうなぁ、とは分かるはずですけどね。


というわけで、SiとCuでは、Siの方が酸化されやすい。


さあ、次は反応熱です。

えっ、反応熱？？？　グラフの縦軸にも横軸にも反応熱なんて書いてねーよ！！！
なんて焦ってはいけません！　テンパったら、そこでアウトですからね！
落ち着いて、最初の文章（問題編22ページ）を読んでみましょう。

第2パラグラフの最初に次のように書いてあります。

『化学熱力学では反応熱を反応のエンタルピー変化で表す。』

そうです！　グラフの縦軸からギブズエネルギーの値が分かりますから、
エンタルピーを求めることができるんですね！

さて、ギブズの定義は…

ΔG_ｒ = ΔH_ｒ - TΔS_ｒでしたね。

エンタルピーを求めたいのですが、エントロピーという邪魔な値が存在します。
エントロピーを無視するにはどうしたらいいか？

絶対温度を0Kにしてしまえばいいですね！


このことは、結局、エリンガム図において、直線を0Kのところまで伸ばす（＝外挿する）
といいことが分かります。




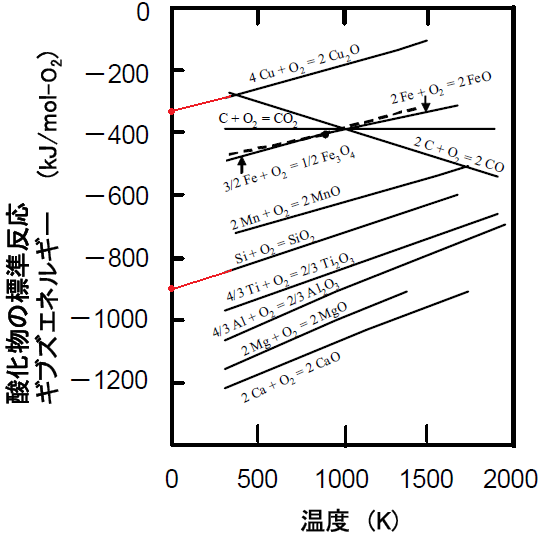
Siの方はΔH_ｒ°= -900 (kJ mol^-1)でよいでしょうが、
Cuの方は微妙ですね。。。私の外挿がヘタクソなのか、私には-330に見えます。
公式の解答では、-320にならないといけないようですが、少々ずれでも、減点はないでしょう。

さて、これで安心して、反応熱→ -900kJ mol^-1と解答欄に書いていいのでしょうか。

いいわけないですね。

そもそも、反応熱がマイナスということは吸熱ということですよ！
アルミニウムを燃やす反応は吸熱ですか？

実は、テルミット反応のあの火花のように見えるものは、周囲から熱を奪っていたのですか？

そんなはずはありません。
発熱反応のハズですよね。


慌てず騒がず、最初の文章（問題編22ページ）を読んでみると、

2パラの最後に、

『吸熱反応に対してはΔH_ｒ°＞ 0，発熱反応に対してはΔH_ｒ°＜ 0 となる』

と書いてあります。

Δは変化量を表しているだけですからね。

というわけで、これで本当に安心して、解答欄を埋めることができますね。

答え。それぞれの反応の1 bar におけるO₂(g) 1 モル当たりの発熱量（反応熱）は、
Si → 9.0×10² kJ
Cu → 3.2×10² kJ

有効数字のミスはしたくありませんね。

もちろん、単位を［J］に変換してもOK。

 

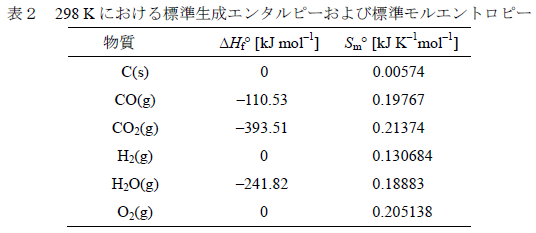
問８　1 モルの O2(g) と化合する元素および生成した酸化物が凝縮相（固体または液体）である 　場合，各直線の傾きはほぼ等しくなる。また，C(s)が1 モルのO2(g)と反応してCO2(g)を生成する 　場合の直線は水平，CO(g)を生成する場合はほぼ同じ大きさで逆の傾きをもつ。 (1) 表２のデータを用いて，C(s)が酸化されてCO2(g)を生成する反応およびCO(g)を生成する反応 　の標準反応エンタルピー，標準反応エントロピーの値をそれぞれ求めなさい。 (2) 反応(10)に対応する直線の傾きがほぼ同じとなる理由を答えなさい。

問8　もう大丈夫でしょう。（右辺）-（左辺）ですね。

（1）CO₂の場合
C(s) + O₂(g) → CO₂(g)

ΔH_ｒ°= -393.51 - 0 = -393.51 ≒ -393.5 (kJ)
ΔS_ｒ°= 0.21374 - (0.00574+0.205138) = 0.002862 (kJ K^-1)


COの場合
2C(s) + O₂(g) → 2CO(g)

ΔH_ｒ°= -110.53 x 2 - 0 = -221.06 ≒ -221.1 (kJ)
ΔS_ｒ°= 0.19767 x 2 - (0.00574 x 2 +0.205138) = 0.178722 ≒ 0.1787 (kJ K^-1)


（2）←解答用紙では（3）になってる。

直線の傾きは何を表しているのか、をまずは考えていきましょう。


先程の問7を思い出してみてください。

ギブズの定義より、
ΔG_ｒ = ΔH_ｒ - TΔS_ｒ

ここで、ΔH_ｒ °はy切片。Tは変数ですから、

グラフの傾きは　-ΔS_ｒ °となりますね。

ここで、ちょっと待った―、という人がいるでしょう。
グラフはどう見ても右上がり！
ということは、グラフの傾きはΔS_ｒ °ではないのか、と。

ご安心ください（!?）

反応（10）においては、ΔS_ｒ °はマイナスの値になっていますから、
グラフの傾きとしてはきちんとプラスになるんですね！


さて、以上のように、グラフの傾きは　-ΔS_ｒ °となることが分かりました。

ところで、そもそもΔS_ｒ °って何だったでしょうか？

慌てず騒がず、最初の文章（問題編22ページ）を読んでみると、（コピペ）

3パラの最初に、

『物質の集合状態の乱雑さを表すエントロピー』

と書いてありますね！


ここで、問題をもう一度眺めてみると、

『1 モルの O₂(g) と化合する元素および生成した酸化物が凝縮相（固体または液体）である場合，』

という、以下にも意味ありげな文章が目に入ります。


気体では、エントロピー（≒乱雑さ）は当然大きいですが、
凝縮相においては、小さいですよね！

ここら辺をヒントにして理由説明を考えていきます。


注目すべきは、気体の酸素は、金属との反応により消費され、
凝縮相である酸化物になってしまうという点です。

反応において、エントロピー（≒乱雑さ）は小さくなっていますね。


ここで、エリンガム図を眺めてみると、
素晴らしいことに、各反応において、消費された酸素のモル数（物質量数）は一定にしてあります！

これこそが直線の傾きがほぼ同じになる理由ですね。


以上をうまくまとめましょう。

公式の解答を部分的に（ほとんど？）パクって書くと、

各直線の傾きは、-ΔS_ｒ °と考えてよく、酸素以外が凝縮相の場合、
各反応において気体1molが消滅するので、そのエントロピー変化はほぼ一定になるため。

 

問９　エリンガム図から，2CO(g) + O2(g) → 2CO2(g)の反応に対応する直線を図中に描きなさい。 　また，1000 K において，CO(g)を流してFeO(s)を還元した場合，反応に使われるCO(g)の割合を 　有効数字 1 桁で答えなさい。 ▼　解答用紙の図（実物大）

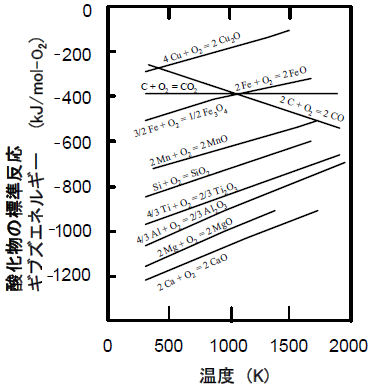
問9　まずは、表2から　2CO(g) + O₂(g) → 2CO₂(g)　の反応に対応する
ΔH_ｒ°とΔS_ｒ°の値を求めましょう。

ΔH_ｒ°= -393.51 x 2 - (-110.53) x 2 = -565.96 ≒ -566.0 (kJ)
ΔS_ｒ°= 0.21374 x 2 - (0.19767 x 2 + 0.205138)=  -0.172998 ≒ -0.1730 (kJ K^-1)

すると、驚くべきことに、

2C(s) + O₂(g) → 2CO(g)　の反応の
ΔS_ｒ°=  0.1787 (kJ K^-1)

の傾きをマイナスにしたものとほぼ同じであることが分かります！

これは、もしかして…、



C + O₂ → CO₂　の反応の直線に対して、
2C + O₂→ 2CO　の反応の直線と線対称の直線が引けました！

なんたる偶然！

…でも、よく考えると当たり前ですよね。

2C + O₂→ 2CO　の反応の直線と　2CO + O₂ → 2CO₂　の直線を足して2で割った直線が
C + O₂ → CO₂　の反応の直線にならなかったらイヤですもんね。

といふわけで、

＜別解＞

Cの酸化を表す2本の直線から、求める反応の直線は、……図の通り。


続きの問題。

先程の図（↓）を見てみると、何ということでしょう！

1000Kにおいて、2CO + O₂ → 2CO₂　の直線と　2Fe + O₂ → 2FeO　の直線が交わっています！




COを流して、FeOを還元させているので、2式より、

FeO + CO → Fe + CO₂

この反応が2直線の交点においては平衡状態に達しているので、

FeO ： CO ： Fe ： CO₂ = 1 ： 1 ： 1 ： 1　になっています。

∴平衡状態において、CO ： CO₂ = 1 ： 1

よって、50%のCOが反応して、CO₂になることが分かります。

さて、ここで有効数字1桁と書いてあるので、私としては、答えは 5×10 ％ と書きたい。

とはいえ、へんてこなので、50％と書いても大丈夫なんでしょうかね。
公式の解答ではそうなってますしね。



以上が2007年度の【4】でした。最後の数問を除いては、
それほど難しくはなかったと思いますが、何しろ、この年は全体の問題量が多かったので、
時間に泣いた人が多かったのではないでしょうかね。

私も泣きました。（笑）

 

Back ←水性ガスシフト反応	Top 「挑戦！化学グランプリ！（一次選考・筆記）」 Top Page へ
	Home	Λ　一番上に戻る　Λ