途中から「化学平衡」の理解が必要になりますね。
問４ 水性ガスシフト反応は工業的に重要な反応で CO の除去および
H2/CO
比の調整法として
用いられている。以下の各設問に答えなさい。ただし，ΔHｆ°
およびΔSr° の温度依存性は
無視できるとする。
CO(g) +
H2O(g) 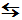 CO2(g) +
H2(g) (8)
(1)
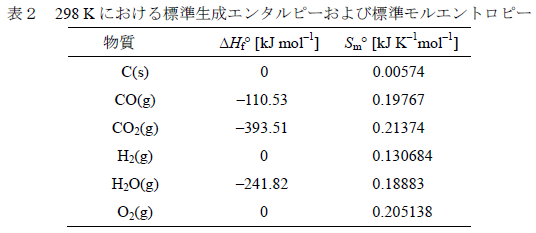
表２のデータを用いてこの反応の298 K
における標準反応エンタルピー，標準反応エントロピ
ーおよび標準反応ギブズエネルギーを求めなさい。
(2)
密閉された容器の中で等モルのCO(g)およびH2O(g)を反応させる。反応したCO（またはH2O）
の割合（反応率）を
a とするとき，平衡定数と a の関係を示しなさい。
(3) 平衡状態における反応率が
0.9 となるときの温度を求めなさい。
（log 3 =
0.4771、気体定数 R =
8.314 J mol-1 K-1
） |
| |
問4（1） 今までの問題と同じように式を立てます。
（生成系）−（反応系）でしたね！ 要は、（右辺）−（左辺）をします。
ΔHｒ°=
ΔHｆ°(CO2) + ΔHｆ°(H2) - ｛
ΔHｆ°(CO) + ΔHｆ°(H2O) ｝
= -393.51 + 0 -
｛ -110.53 + (-241.82)
｝
=
-41.16（kJ）
エントロピーも同様に、
ΔSｒ°=
Sm°(CO2) + Sm°(H2) - ｛
Sm°(CO) + Sm°(H2O) ｝
= 0.21374 +
0.130684 - ( 0.19767 + 0.18883 )
=
-0.042076
≒ -0.04208（kJ K-1）
もしくは、カッコよく、-4.208×102（kJ
K-1）
としてもいいですね。
ギブズエネルギーは、ΔGｒ =
ΔHｒ - TΔSｒ より、
ΔGｒ°= -41.16 -
298 × ( -0.042076 )
=
-28.621352
≒ -28.62（kJ）
(2) さあ、化学平衡ですよ！
表で整理すると、以下のようになります。
反応前のCOの物質量（モル数）をn［mol］とすると、
|
|
CO(g) |
H2O(g) |
CO2(g) |
H2(g) |
|
反応前 |
n |
n |
0 |
0 |
|
（反応中） |
-an |
-an |
+an |
+an |
|
反応後 |
(1-a)n |
(1-a)n |
an |
an |
平衡定数Kは、（生成系）/（反応系）、つまり（右辺）/（左辺）で表されますね！
よって、反応後の平衡定数は、
K = a2n2 /(1-a)2n2
= a2 /(1-a)2
= ( a/1-a )2
（3） a =
0.9のとき、（2）の答えに代入すると、
K = ( 0.9/1-0.9 )2 =
81 となるので、
log K =
log 81 = log 34 = 4 log
3 となります。
ここで、log 3 = 0.4771 と与えられているので、
log K =
1.9084 となります。
＜ありがちな間違い その1＞
（1）より、ΔGｒ°=
-28.62（kJ）なので、
（1）は温度を勝手に298Kと定義して求めたギブズエネルギーなので計算に用いてはいけない。
さらに、式に代入するときには、有効数字+1ケタ！
＜ありがちな間違い その2＞
-ΔGｒ°= 2.303RTlog
K 、 ΔGｒ = ΔHｒ - TΔSｒ より
2.303RTlog K = -（ΔHｒ°-
TΔSｒ°）
2.303RTlog K - TΔSｒ°= -ΔHｒ°
T (
2.303Rlog K - ΔSｒ°) = -ΔHｒ°
T ( ΔSｒ°-
2.303Rlog K ) = ΔHｒ°
T = ΔHｒ°/ ( ΔSｒ°-
2.303Rlog K )
ここまではあってますね。
さて、ここで、
ΔHｒ°= -41.16（kJ）
ΔSｒ°= -0.042076（kJ K-1）
R =
8.314 (J mol-1 K-1）
log K =
1.9084
を代入して……
問3でもありましたが、単位を[kJ]にそろえるために、
R = 8.314
x
10-3
( kJ mol-1 K-1
) として代入しなければなりません。
この値で代入すると、
T = -41.16 / -0.042076 - 2.303 x
8.314 x 10 -3 x
1.9084
≒
523.55
≒
523.6（K）
問５ コークスから水性ガスを製造する際の反応は次のように表される。
C(s)
+ H2O(g) 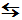CO(g) +
H2(g)
(9)
この反応を密閉された容器の中で行うとし，初めに十分な量のC(s)と1
bar のH2O(g)のみが容器
内にあったとする。H2O(g)の反応率をa
とするときこの系の平衡定数K とa の関係を示しなさい。
また，平衡状態における反応率が0.9
以上となるためには温度を何度以上にすればよいか答えな
さい。
（log 3
= 0.4771、気体定数 R = 8.314 J mol-1
K-1
）
|
|
問5 炭素は十分にあるので、無視して考えることができるので、
反応前のH2Oの物質量（モル数）をn［mol］とすると、
|
|
H2O(g) |
CO(g) |
H2(g) |
|
反応前 |
n |
0 |
0 |
|
（反応中） |
-an |
+an |
+an |
|
反応後 |
(1-a)n |
an |
an |
よって、反応後の平衡定数は、
K = a2n2 /(1-a)n
= a2 / 1-a
あとは、問4とまったく同様に計算するだけです。
ただし、エンタルピー、エントロピーの計算においては、炭素を省略してはいけません。
炭素も反応系に入っていますからね。
a
= 0.9のとき、K = 8.1 となるので、
log K = log 8.1 = log
(81/10) = log 81 - log 10 = log 34
-1 = 4 log 3 -1 = 0.9084
数II の常用対数での必須手法ですね。
log
2 の値が与えられている場合に、log 5
の値を求めろ、という問題を見たことがあるはず。
また、エントロピー、エンタルピーは、表2の値を使い、
ΔHｒ°= ΔHｆ°(CO) +
ΔHｆ°(H2) - ｛ ΔHｆ°(C) +
ΔHｆ°(H2O) ｝
= 131.25（kJ）
ΔSｒ°=
Sm°(CO) + Sm°(H2) - ｛
Sm°(C) + Sm°(H2O) ｝
=
0.133784
≒ 0.13378（kJ K-1）
-ΔGｒ°= 2.303RTlog K 、 ΔGｒ =
ΔHｒ - TΔSｒ より
2.303RTlog K =
-（ΔHｒ°-
TΔSｒ°）
2.303RTlog K - TΔSｒ°= -ΔHｒ°
T (
2.303Rlog K - ΔSｒ°) = -ΔHｒ°
T ( ΔSｒ°-
2.303Rlog K ) = ΔHｒ°
T = ΔHｒ°/ ( ΔSｒ°-
2.303Rlog K )
種々の値を代入して、
T = 131.25 / 0.13378 - 2.303 x 8.314
x 10-3 x
0.9084
≒
1127.7
≒ 1128（K）
それにしても、公式の解答では、この問4、問5と
気体定数 R を 8.3145
として計算していますが、
問題冊子に書かれていないはずの小数第4位がなぜ分かったのでしょうね。
問６ 次の各反応の標準反応ギブズエネルギーが次のように与えられているとき，各金属イオン
の標準生成ギブズエネルギーを求めなさい。また，各金属の酸化されやすさの序列を示しなさ
い。ただし，H+(aq)の標準生成ギブズエネルギーは0
とする。
（ア）
Cu2+(aq) + Zn(s)
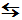Cu(s) + Zn2+(aq)
ΔGr
° = -212.55 kJ
（イ）
2H+(aq) + Fe(s) 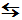H2(g) +
Fe2+(aq)
ΔGr ° = -78.90
kJ
（ウ）
Fe2+(aq) + Zn(s)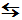
Fe(s) + Zn2+(aq) ΔGr ° =
-68.16 kJ
（エ）
Pb2+(aq) + Zn(s)
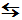Pb(s) + Zn2+(aq)
ΔGr
° = -122.63
kJ |
|
問6 金属の酸化されやすさなんて、イオン化列を覚えていれば楽勝さ！
ということで、序列だけは、すぐに書くことができますが、
ちゃんと計算を要求しているところがニクいですねぇ。
H+(aq)の標準生成ギブズエネルギーが基準となっているので、
まずは（イ）より、
ΔGf°(H2) + ΔGf°(Fe2+) - { 2ΔGf°(H+) + ΔGf°(Fe) } =
ΔGr°となりますが、
「標準状態における単体の標準生成ギブズエネルギーは0とする」、
および「H+(aq)の標準生成ギブズエネルギーは0 とする」とあるので、
実質、ΔGf°(Fe2+) =
ΔGr°となるので、
ΔGf°(Fe2+) =
-78.90（kJ mol-1)
となります。
同様に、（ウ）においても、
実質、ΔGf°(Zn2+)
- ΔGf°(Fe2+) =
ΔGr°となるので、
ΔGf°(Zn2+)
= -68.16 +
(-78.90)
=
-147.06 （kJ mol-1)
（ア）では、
実質、ΔGf°(Zn2+)
- ΔGf°(Cu2+) =
ΔGr°となるので、
ΔGf°(Cu2+)
= -147.06 -
(-212.55)
=
65.49（kJ mol-1)
（エ）は、
実質、ΔGf°(Zn2+)
- ΔGf°(Pb2+) =
ΔGr°となるので、
ΔGf°(Pb2+)
= -147.06 -
(-122.63)
=
-24.43 （kJ mol-1)
ここで、ギブズエネルギーが小さくなる方向に反応は進むので、
金属の酸化されやすさは以下のようになります。
Zn ＞ Fe ＞ Pb ＞ (H2) ＞Cu
計算量が多く、途中、引っ掛かりそうな箇所がいくつかありますが、
考え方自体はそんなに難しいものではありません。
時間があれば、きちんと解けるのでしょうが…。
つづく。
