Location:　Home > 挑戦！化学グランプリ！ >  1次（筆記） > 魅せるぜ！ミセル！ ['07-1-3a]



【３】は、主に無機化学に関する問題です。
今年の問題はA〜Cのパートで構成されていました。

化学グランプリの問題は、きちんと読めば、大部分は解けるはずなので、
まずは問1まで問題を読んでみて下さい。

　
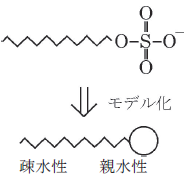
[Ａ]
　 一般に水と油は互いに溶け合うことはないため，両者を混合すると二層に分離するのが観察される。ここに，セッケン液を入れて振ると，今まであった明確な境界線はなくなり，あたかも水と油が溶けあったかのような状態となる。このように，水と油の界面に作用する溶質のことを界面活性剤といい，洗浄などの分野でよく用いられる。
　 界面活性剤としてはたらくイオンや分子には，疎水性（油に対して親和性を持つ）の部分と，親水性（水に対して親和性をもつ）の部分がある。界面活性剤の代表的なものに，ドデシル硫酸ナトリウムCH3−(CH2)11−OSO3− Na+がある。ドデシル硫酸ナトリウムは，水に溶解すると電離し，親水性の官能基が陰イオンに電離するため，アニオン性界面活性剤（アニオンとは陰イオンのことを指す）とよばれる。ここでは，ドデシル硫酸イオンを以下のように略記する。
 

　
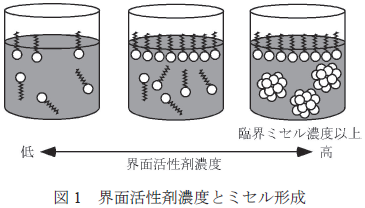
　 ドデシル硫酸ナトリウム水溶液では，ドデシル硫酸イオンは親水性部分を水側に，疎水性部分を空気側に向けてその界面に集まることが知られている。その濃度を高めていくと，界面がドデシル硫酸イオンによって覆われた，単分子層という層が形成される。一方，溶液の内部では，イオンどうしが集まってミセルとよばれる集合体を作りはじめる。ミセルが急激に増加すると考えられる濃度を臨界ミセル濃度といい，これを境として溶液の性質が大きく変わる。
 


　 実験により，ドデシル硫酸ナトリウム水溶液の抵抗を測定し，臨界ミセル濃度を求めた。
操作1 濃度の分かっている数種類のドデシル硫酸ナトリウム水溶液を調製した。
操作2 以下の図2 のような回路を構成した。交流電源に接続し，ドデシル硫酸ナトリウム溶液中の
　　電極間に電圧をかけて微弱な電流を流した。可変抵抗器を動かし，検流計の針が触れない位
　　置を探し，そのときの電気抵抗 R1，R2 [Ω]を記録した。水溶液の電気抵抗をRX [Ω]とすると，
　　R1 × RX ＝ R2 × R3 の関係があることを利用し，RX を求めた。なお，この操作における可
　　変抵抗器とは，電気抵抗（R1＋R2 ）の値を一定に保ちつつR1，R2 を変えることのできる装置で
　　ある。ここでは，電気抵抗R3 ＝ 111Ωで固定されている。
 


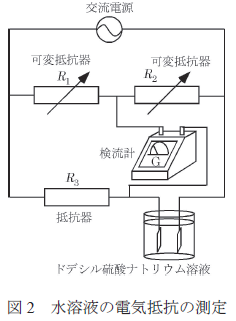
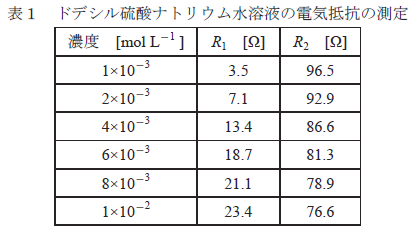
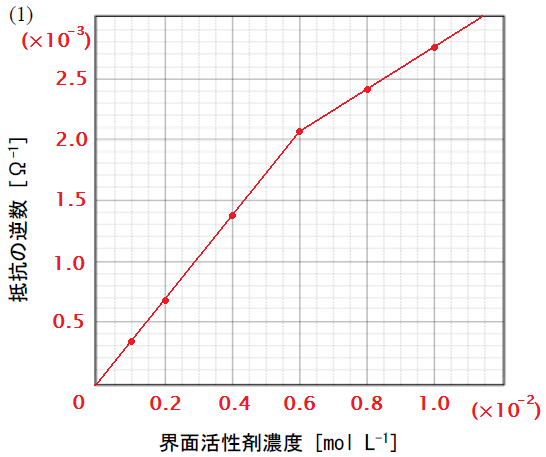
問１　この実験を行ったところ，以下の表1 のデータが得られた。
(1) 横軸に界面活性剤濃度 [mol L-1 ]，縦軸に電気抵抗RX の逆数 [Ω-1 ]をとり，グラフを描きな
さい。
(2) 臨界ミセル濃度の前後で，RX の変化の傾向に違いがみられる。グラフから，臨界ミセル濃度
[mol L-1 ]を求めなさい。
 





問1（1）に関しては、ちょうど下ぐらいの大きさの解答欄が与えられるので、
これに自分で軸の数値も書き込んで解答するわけです。




さて、解法ですが、問題の指示通り、RX の逆数を求めましょう。
問題文中に、「水溶液の電気抵抗をRX [Ω]とすると，R1 × RX ＝ R2 × R3 の関係がある」、
さらに、「電気抵抗R3 ＝ 111Ωで固定されている」と明記されているので、
R1 × RX ＝ R2 × R3
1/RX ＝R1 / R2R3
R3 ＝ 111（Ω）より、 1/RX ＝ R1 / (111×R2 )
と表せます。

あとは、表にある数値を代入するだけですね。
「R1 ＝ 3.5　R2 ＝ 96.5 を代入？　そんな計算できるか！」と思ったあなた！
ご安心ください！　化学グランプリに参加すると、電卓が無料で貰えます！　
電卓を使って問題が解けるので、計算が遅い人でも安心です！
それでは、電卓を使って解いてみましょう。

濃度が 1×10-3 （mol L-1）のとき、R1 ＝ 3.5（Ω）　R2 ＝ 96.5（Ω）なので、
 1/RX ＝ R1 / (111×R2 ) に代入して、 1/RX ≒ 0.0003267 ＝ 3.267×10-4 （Ω-1） と求まりましたね。
同様に、濃度が 2×10-3 （mol L-1）のとき、1/RX ≒ 3.267×10-4  （Ω-1）
 　　　　　　　　　 4×10-3 （mol L-1）のとき、1/RX ≒ 6.885×10-4  （Ω-1）
 　　　　　　　　　 6×10-3 （mol L-1）のとき、1/RX ≒ 1.394×10-3  （Ω-1）
 　　　　　　　　　 8×10-3 （mol L-1）のとき、1/RX ≒ 2.409×10-3  （Ω-1）
 　　　　　　　　　 1×10-2 （mol L-1）のとき、1/RX ≒ 2.752×10-3  （Ω-1）

次に、上で求まったデータをグラフ上にプロットします。

軸の目盛の数字は、2×103 、4×10-3 といちいち書いていってもいいのですが、
めんどくさい上に見にくくなるので、横軸は×10-2、縦軸は×10-3 でまとめました。




そして、点を結ぶわけですが、少々ずれても構わないので、滑らか（今回は直線）に結びましょう。

続いて、（2）の問題です。
「臨界ミセル濃度の前後で，RX の変化の傾向に違いがみられる。」
グラフより、0.6×10-2（mol L-1）の前後で、グラフの傾きに違いがみられますね。
ここが臨界ミセル濃度にあたります。

∴ 0.6×10-2 ＝ 6×10-3（mol L-1）


続いて、問2、問3を解いてみましょう。


　
問２　ドデシル硫酸イオンは，臨界ミセル濃度以上では，球状のミセルを形成する。これを図３の
ようにモデル化する。また，別の実験により，このモデルにおいて，親水性部分の占める表面積
S ＝ 0.580 nm2 ，ドデシル硫酸イオンの長さr ＝1.67 nm であることがわかっている。このとき，
ミセル1 個に含まれるドデシル硫酸イオンの個数（これを凝集数という）を整数で求めなさい。
（円周率 π＝3.14 とせよ。）






球の表面積は 4πr2 で求めることができるので、

4×3.14×（1.67）2 / 0.58 ≒ 60.3 ≒ 60（個）


　
問３　臨界ミセル濃度以上では，過剰なドデシル硫酸イオンが問２のようなミセルを形成していると仮定する。ミセルを一つの粒子として考えたとき，0.080 mol L-1 のドデシル硫酸ナトリウム水溶液中に含まれるミセルの濃度は何mol L-1 か，有効数字2桁で求めなさい。



「臨界ミセル濃度以上では，過剰なドデシル硫酸イオンがミセルを形成」
＝「臨界ミセル濃度を超える分のイオンがすべてミセルを形成」

と考えます。限界ミセル濃度は問1（2）より、 6×10-3 ＝ 0.006（mol L-1）ですから、
0.080 - 0.006 ＝ 0.074 （mol L-1）のドデシル硫酸イオンがミセルを形成するわけです。

ここで、問2より、ミセル1個あたりのドデシル硫酸イオンの数は60個なので、
0.074 / 60 ≒ 0.00123 ≒ 1.2×10-3 （mol L-1）

もともと、mol という単位は 6.02×1023 個 を表してるわけですから、
60（個）で割っても、別に違和感を感じる必要性はありませんね。



ここまでがAパートでした。
問題はBパートへと続くのです。




Top
「挑戦！化学グランプリ！（一次選考・筆記）」 Top Page へ


Next
水はみんなのもの→

Back
←【2】 有機化合物の様々な合成プロセス


Home

Λ　一番上に戻る　Λ