【4】は、主に物理化学(今回は、化学熱力学)に関する問題です。
化学グランプリの問題は、きちんと読めば、大部分は解けるはずなので、
まずは問1まで問題を読んでみて下さい。
|
次の文章を読み,以下の問1〜問9に答えなさい。なお,解答の数値については指定したもの以外有効数字4桁まで求めなさい。 | |
有効数字4桁!!
これが化学グランプリの最大の特徴の一つかもしれません!
計算は苦手だよ…、という方もご心配なく!
化学グランプリに参加すると、電卓が無料で貰えます!
電卓を使って問題が解けるので、計算が苦手な人でも安心です!
各設問で同じようなことを書いてますが、あまり気にしないように。(笑)
炭酸水素ナトリウム(NaHCO3)は重曹とも呼ばれ,パンや菓子を作るときに用いられるベーキングパウダーの主成分である。炭酸水素ナトリウムは常温では固体であるが,加熱すると次のような反応で分解し,最終的には炭酸ナトリウム,水および二酸化炭素を生成する。
2NaHCO3(s)
→ Na2CO3(s) + H2O(g) +
CO2(g)
(1)
この反応は吸熱反応であり,298Kにおける熱化学方程式は次の通りである。
2NaHCO3(s)
= Na2CO3(s) + H2O(g) +
CO2(g) - 136.57kJ
(2)
反応熱は化学結合の組み替えに伴って放出または吸収されるエネルギーであり,化学反応は物質のエネルギーが減る方向,すなわち発熱する方向に自発的に進みやすいと考えられる。しかし,実際には吸熱反応であっても自発的に進む反応はあり,反応の自発性は反応熱のみから判断することは一般にできない。
化学熱力学では反応熱を反応のエンタルピー変化で表す。ある温度での標準状態(化学熱力学において標準状態とは圧力が
1bar(1000hPa)の状態のことをいい,温度は指定されない。)における生成系(右辺)と反応系(左辺)のエンタルピーの差を標準反応エンタルピー(ΔHr°)と呼ぶ。また,ある物質
1mol
をそれを構成する元素の標準状態にある単体から生成する反応の標準
反応エンタルピーを特に標準生成エンタルピーと呼び,ΔHf°で表す。なお,標準状態における単体の標準生成エンタルピーは0
とする。例えば,反応(1)に対しては(3)式のように書ける。
ΔHr° =
ΔHf°(Na2CO3) +
ΔHf°(H2O) +
ΔHf°(CO2) -
2ΔHf°(NaHCO3)
(3)
この反応に関与する物質の標準生成エンタルピーを用いて計算すると,ΔHr°= 136.57
kJ となり,吸熱反応に対してはΔHr°> 0,発熱反応に対してはΔHr°< 0
となることがわかる。
反応の自発性を判断するためには物質の集合状態の乱雑さを表すエントロピーという量を考え
る必要がある。一般に状態の変化は乱雑になる方向に進みやすく,そのときエントロピーは増大
する。標準反応エントロピーは,ある温度での標準状態における生成系と反応系のエントロピーの差であり,ΔSr°で表される。反応(1)に対しては,(4)式のように計算することができる。
ΔSr°=
Sm°(Na2CO3) +
Sm°(H2O) +
Sm°(CO2) -
2Sm°(NaHCO3)
(4)
各物質の標準モルエントロピーSm°を用いて計算すれば,ΔSr°=
0.33332 kJ K-1
となり,生成系のエントロピーの方が反応系よりも大きいことがわかる。
ギブズ(J. Gibbs,
1839-1903)は反応の自発性を示す量として,反応のギブズエネルギー変化
ΔGrを次の(5)式のように定義した。
ΔGr
= ΔHr - TΔSr
(5)
ここでT
は絶対温度である。エンタルピーの場合と同様に,標準状態における単体の標準生成ギ
ブズエネルギーを0
として,標準生成ギブズエネルギーΔGf°および標準反応ギブズエネルギー
ΔGr°を定義することができる。また,標準反応ギブズエネルギーは反応の平衡定数K
と結びつけることができ,気体定数をR とすると次のようになる。
-ΔGr°=
2.303RTlog K
(6)
この関係を用いれば,与えられた反応が平衡状態でどのような組成となるかを知ることができる。
|
問1 反応(1)の298 K
における標準反応ギブズエネルギーの値を計算しなさい。
|
|
問1 標準反応ギブズエネルギーは(5)の公式より
ΔGr =
ΔHr - TΔSr
ですから、この式に値を代入していくだけです。
この式には
°が付いていませんが、「それはおそらく“標準(状態)”の意である」と
文章から判断できるでしょう。
というわけで、文章中より、ΔHr°=
136.57 kJ 、ΔSr°= 0.33332 kJ K-1
設問の条件より、T = 298 K ですから、
ΔGr° = 136.57 -
298×0.33332 を(電卓で)計算すれば答えが出てきます。
∴ΔGr°≒ 37.24
(kJ)
問2 反応(1)の平衡定数 K が K≧1
となる温度を求めなさい。ただし,標準反応エンタルピー
および標準反応エントロピーの温度依存性は無視できるとする。
(ただし、気体定数
R = 8.314 J mol-1 K-1とする
) |
|
問2 今度は(6)を利用します。
-ΔGr°= 2.303RTlog
K
問題の条件より、K≧1ですから、log K≧0
ですね?
分からない人は、数IIの教科書で復習してください。
指数・対数は、センターでも毎年出題されますよ!!
問1と同じように、ΔGr°=
ΔHr°- TΔSr°を代入して、
-(ΔHr°- TΔSr°)= 2.303RTlog
K
(-ΔHr°+ TΔSr°)/ 2.303RT = log K
log
K≧0ですから、 (-ΔHr°+ TΔSr°)/ 2.303RT ≧0
両辺を
2.303RT倍して、 -ΔHr°+ TΔSr°≧0
T ≧ ΔHr°/
ΔSr°
ΔHr°= 136.57 kJ 、ΔSr°= 0.33332 kJ
K-1 を代入して、
T ≧
136.57 / 0.33332
T ≧
409.7(K) (絶対温度をTとする)
これが答えです!
公式の模範解答では、409.7Kが答えになっていますが、これは間違いです!
K≧1
となる温度を求めるのですから、409.7K以上という答えじゃないとおかしいですよね。
また、Tの条件を求めたいからといって、以下のように、Tについて整理してもいいですが…、
-(ΔHr°-
TΔSr°)= 2.303RTlog K
TΔSr°- 2.303RTlog
K=ΔHr °
T(ΔSr°-2.303Rlog
K)=ΔHr°
T=ΔHr° /(ΔSr°-
2.303Rlog K)
ΔHr°= 136.57 kJ 、ΔSr°= 0.33332
kJ K-1、R = 8.314 J mol-1
K-1 を代入して、
T = 163.57/(
0.33332 - 2.303 ・ 8.314 ・ logK)
y =
logKのグラフは、単調増加するので、
logKが最小値をとるとき、Tは最小値をとる。
∴K≧1における最小値0を代入し、
T
= 163.57 / 0.33332 ≒ 409.7
∴絶対温度をTとすると、T ≧
409.7(K)
ちょっと数学的に問題がある方法かな?
まあ、答えが出ればいいんですけどね。
問3 共に1価のイオンからなる難溶性塩AX
の溶解平衡は次式で表される。
AX (s) 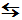 A+ (aq) + X-
(aq) (7) A+ (aq) + X-
(aq) (7)
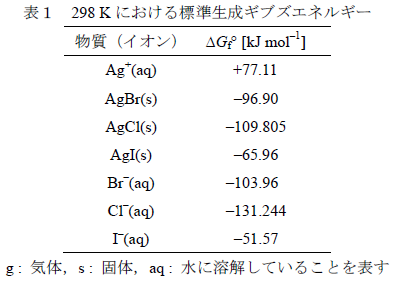
この平衡定数は[A+ (aq)][X- (aq)]となるので,これを溶解度積 Ksp
と呼ぶ。表1の値を用いてAgCl,AgBr およびAgI のlog Ksp
の値を計算し,溶解度の大きな順に並べ替えなさい。なお,温度は298K とする。
(ただし、気体定数 R =
8.314
J mol-1 K-1とする
) |
|
|
問3 (3)〜(5)式より、
ΔGr°= ΔGf°(A+) + ΔGf°(X-) -
ΔGf°(AX)
(6)式より、
-ΔGr°= 2.303RTlog
Ksp
まとめて、 ΔGf°(A+) + ΔGf°(X-) - ΔGf°(AX) = - 2.303RTlog
Ksp
∴ log Ksp = { ΔGf°(AX) -
ΔGf°(A+) -
ΔGf°(X-) }/ 2.303RT
T
= 298 K 、 R = 8.314 J mol-1 K-1 = 8.314
×10-3 kJ mol-1
K-1 を代入し、
ここがこの問題最大の注意点です!
ΔGr°の単位は、[kJ]ですから、当然、kJに単位をそろえなければなりません!
∴
log Ksp = { ΔGf°(AX) - ΔGf°(A+) - ΔGf°(X-) }/
5.7058
あとは、表の値を代入していくだけです。
AgCl の log Ksp は、{ -109.805 - 77.11 - (-131.244)
} / 5.7058 ≒ -9.757
AgBr の log Ksp は、{ -96.90 - 77.11 - (-103.96) }
/ 5.7058 ≒ -12.28
Ag I の log Ksp は、{ -65.96 -
77.11 - (-51.57) } / 5.7058 ≒ -16.04
さて、残された問題は、log Ksp
が大きいほど、溶解度は大きくなるのか、小さくなるのか、ということです。
ちょっと厄介な問題なので、グラフを使って考えてみましょう。
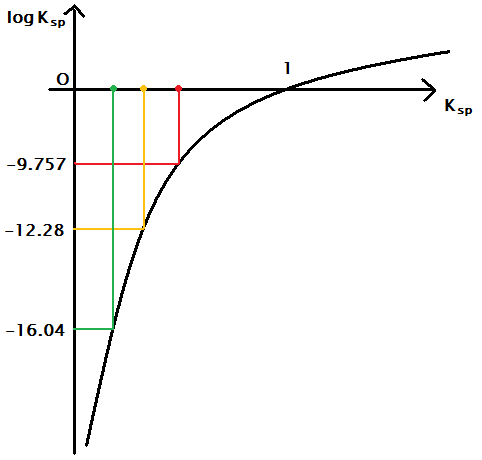
↑のグラフのように、Ksp の値は、AgI <
AgBr < AgCl の順になります。
ここでの溶解平衡は、(7)式より、
AX (s) 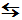 A+ (aq) + X-
(aq) ですから、
A+ (aq) + X-
(aq) ですから、
Ksp
の値が大きいということは、右向きの反応速度が大きい、つまり溶解しやすいということになります。
つまり、log
Ksp
の値は小さい方が溶解しやすいのです。
水素イオン濃度とpH の関係と同じというわけですね。(そりゃそうか。)
したがって、溶解度は、AgCl > AgBr > AgI
の順になります。
以上、エントロピー、エンタルピー、ギブズエネルギーの定義と
それらに慣れるための問題でした。
この後の問題では、さらに実践的な問題になっていきます。
つづく。

![]() A+ (aq) + X-
(aq) ですから、
A+ (aq) + X-
(aq) ですから、